| Issue |
ITM Web Conf.
Volume 34, 2020
International Conference on Applied Mathematics and Numerical Methods – third edition (ICAMNM 2020)
|
|
|---|---|---|
| Article Number | 03010 | |
| Number of page(s) | 14 | |
| Section | Differential Equations, Dynamical Systems, and Geometry | |
| DOI | https://doi.org/10.1051/itmconf/20203403010 | |
| Published online | 03 December 2020 | |
A study of a three-dimensional competitive Lotka–Volterra system
University of Craiova, Department of Applied Mathematics Al I Cuza 13, Craiova 200585, Dolj, Romania
* e-mail: munteanufm@gmail.com
In this paper we will consider a community of three mutually competing species modeled by the Lotka–Volterra system:
where xi(t) is the population size of the i-th species at time t, Ẋi denote 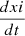 and aij, bi are all strictly positive real numbers.
and aij, bi are all strictly positive real numbers.
This system of ordinary differential equations represent a class of Kolmogorov systems. This kind of systems is widely used in the mathematical models for the dynamics of population, like predator-prey models or different models for the spread of diseases.
A qualitative analysis of this Lotka-Volterra system based on dynamical systems theory will be performed, by studying the local behavior in equilibrium points and obtaining local dynamics properties.
Key words: Dynamical systems / Lotka-Volterra systems / stability
© The Authors, published by EDP Sciences, 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License 4.0, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




